Come abbiamo detto, il più famoso e utilizzato algoritmo di cifratura asimmetrica è RSA, inventato nel 1977 da Ronald Rivest, Adi Shamir e Leonard Adleman (l’acronimo RSA deriva appunto dalle iniziali dei cognomi dei tre inventori).

Nel corso degli anni l’algoritmo RSA ha più volte dimostrato la sua robustezza: in un esperimento del 1994, coordinato da Arjen Lenstra dei laboratori Bellcore, per “rompere” una chiave RSA di 129 cifre, svelando il meccanismo con cui quella chiave generava messaggi crittografati, sono stati necessari 8 mesi di lavoro coordinato effettuato da 600 gruppi di ricerca sparsi in 25 paesi, che hanno messo a disposizione 1600 macchine da calcolo, facendole lavorare in parallelo collegate tra loro attraverso Internet.

Data la mole delle risorse necessarie per rompere la barriera di sicurezza dell’algoritmo RSA, è chiaro come un attacco a forza bruta non sia praticamente realizzabile. Inoltre, nell’esperimento era stata utilizzata una chiave di 129 bit mentre i programmi di crittografia attualmente a disposizione prevedono chiavi private con una “robustezza” che raggiunge e supera i 1024 bit, risultando quindi praticamente inattaccabili.

Uno svantaggio della crittografia a doppia chiave è che le funzioni matematiche che generano il codice cifrato e quelle inverse per decifrarlo fanno si che questo tipo di crittografia sia uno dei più lenti in assoluto (si dice che sia da 100 a 1000 volte più lento dei sistemi simmetrici a singola chiave). Per questo sono nati sistemi di crittografia misti (si veda PGP qui sotto), che combinano algoritmi simmetrici con algoritmi asimmetrici in modo da fonderne i vantaggi. In pratica spesso si utilizza la chiave pubblica soltanto per comunicare la chiave segreta (che in questi casi viene chiamata chiave di sessione) che poi verrà usata per una normale comunicazione basata su cifrati a chiave segreta. In questo modo quindi è ampiamente risolto il problema della sicurezza nello scambio della chiave e la velocità di cifratura/decifratura rimane molto alta e non penalizza la comunicazione.

 

Nel giugno 1991 lo statunitense Philip Zimmermann realizzò e distribuì gratuitamente Pretty Good Privacy (PGP), un programma di crittografia diventato ormai uno standard.

PGP garantisce fra l'altro la segretezza della posta, l’autenticazione con firma digitale e la compressione dei dati. Il software utilizza un sistema di crittografia misto con tre algoritmi: il sistema a chiavi pubbliche RSA, quello a chiavi private IDEA e l’algoritmo di hashing MD5. È distribuito gratuitamente per l’uso personale.

L'utilizzo di due sistemi di cifratura diversi (a chiave privata IDEA e a chiave pubblica RSA) è dovuto al fatto che la cifratura asimmetrica RSA è, come si è detto, piuttosto lenta e richiede risorse di calcolo elevate. In PGP la cifratura RSA viene usata solo per cifrare la chiave (relativamente breve) dell'algoritmo asimmetrico (IDEA). La cifratura vera e propria del messaggio avviene invece usando tale chiave asimmetrica.

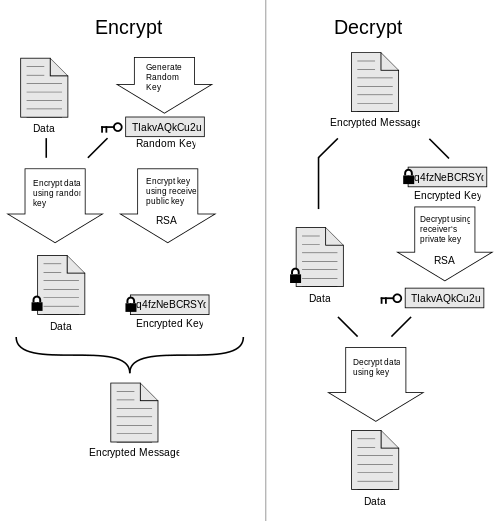
In pratica il suo funzionamento è abbastanza semplice: ammettiamo che l’utente A voglia spedire all’utente B un messaggio. PGP cifra tale messaggio utilizzando l'algoritmo IDEA (un algoritmo simmetrico che non abbiamo qui trattato) con una chiave K generata casualmente. Questa chiave K viene inviata all’utente B, dopo essere stata cifrata con la chiave pubblica di B (con l’algoritmo RSA), insieme al messaggio cifrato con IDEA.

In questo modo solo B può, con la propria chiave Privata, recuperare la chiave K ed usarla per leggere il resto del messaggio. Come detto nella lezione precedente, gli algoritmi a chiave pubblica risolvono anche il problema della firma digitale e con PGP è possibile firmare i messaggi, o meglio una loro sintesi creata tramite l’algoritmo MD5.

Ogni utente del programma, dopo la procedura di installazione, possiede quindi due chiavi, una privata (da mantenere nel proprio PC) e una pubblica. PGP prevede la creazione di archivi pubblici elettronici che contengano le chiavi pubbliche dei vari utenti. In questo modo si può dare la massima diffusione della propria chiave pubblica e consentire a tutti di poter comunicare con noi in modo sicuro.

 

Online RSA Key Generator: un sito online per generare automaticamente una coppia di chiavi pubblica e privata

pidCrypt: cifrare e decifrare con l'algoritmo RSA

 

 

precedente - successiva

Sito realizzato in base al emplate offerto da

http://www.graphixmania.it

Segui @ElePrograMania