Un problema generale è quello della condivisione della chiave fra mittente e destinatario e questa difficoltà diventa ancora maggiore al crescere della lunghezza della chiave usata. Infatti in che modo mittente e destinatario possono scambiarsi la chiave di cifratura/decifratura? Qualsiasi canale di comunicazione usato (per telefono, per lettera, per email, via radio, con un incontro di persona, etc.) presenta problemi di sicurezza e la possibilità che la chiave venga intercettata da qualcuno.

Il problema è che la chiave non può essere a sua volta cifrata, poiché in tal caso bisognerebbe preventivamente accordarsi sull'algoritmo e sulla chiave di cifratura e così via all'infinito. In pratica, mittente e destinatario devono scambiarsi la chiave di cifratura prima di iniziare la corrispondenza e per fare questo devono usare un metodo non cifrato. Per esempio, nel caso semplice del cifrario di Cesare, Cesare potrebbe comunicare a voce la chiave ai propri generali oppure potrebbe inviargliela per mezzo di un messaggero fidato, ma in entrambi i casi la chiave potrebbe essere intercettata da una spia nemica.

Il problema della condivisione delle chiavi è forse la debolezza principale dei sistemi crittografici tradizionali. Questo problema verrà superato soltanto con i sistemi di cifratura moderna, i quali non richiedono due chiavi separate (per crittare e decrittare il messaggio) e non richiedono lo scambio della chiave di decifratura.

In generale dunque si distingue fra:

• crittografia simmetrica: la funzione di codifica e quella di decodifica usano la stessa chiave, o chiavi diverse ma in diretta relazione tra loro (derivazione). Tutti gli esempi visti finora sono crittografie simmetriche, cioè in pratica con un'unica chiave (per cifrare e decifrare il messaggio).
  
  
• crittografia asimmetrica: si usano due differenti chiavi, una per crittare il messaggio (chiave Pubblica) e un'altra per decrittarlo (chiave Privata).

 

Come abbiamo appena detto, gli algoritmi asimmetrici (detti anche a chiave pubblica, per le ragioni che saranno chiare fra poco) presentano la caratteristica di usare due chiavi differenti. Le due chiavi, chiamiamole A e B, possono essere usate alternativamente per cifrare o decifrare un messaggio, nel senso che il messaggio cifrato con A può essere decifrato con B e il messaggio cifrato con B può essere decifrato con A.

Ogni persona coinvolta nello scambio di messaggi possiede dunque una coppia di chiavi che agiscono, di fatto, l'una come l'inverso dell'altra. Una di queste due chiavi viene resa pubblica, cioè nota a tutti. La seconda chiave invece viene mantenuta privata.

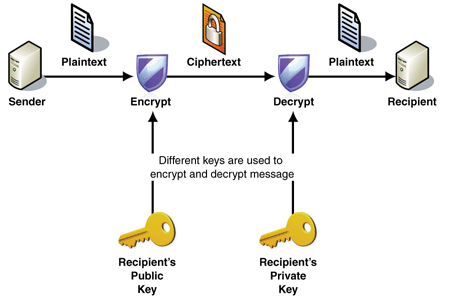
Consideriamo dunque la situazione mostrata in figura in cui un mittente (Sender) deve inviare un messaggio a un destinatario (Recipient). Il messaggio viene crittato usando la chiave pubblica del destinatario (Recipient Public Key): in questo caso non esiste il problema dello scambio delle chiavi, dal momento che, come si è detto, questa chiave è in  linea di principio nota a tutti (potrebbe essere pubblicata anche sull'elenco telefonico). Tuttavia solo il destinatario è in grado di leggere il messaggio, poiché lui solo possiede la chiave privata (Recipient Private Key) per decrittarlo.

 

Facciamo un esempio ancora più concreto, per quanto semplificato. Supponiamo che Bob voglia mandare un messaggio ad Alice e, temendo che questo messaggio venga intercettato, decide di crittarlo. A tale scopo Bob critta il messaggio usando la chiave pubblica di Alice, chiave che Alice può tranquillamente mandargli per email o dettargli per telefono. Infatti questa chiave serve solo per crittare il messaggio, ma è completamente inutile per decrittarlo. Dunque, anche se cadesse in mani "nemiche" la chiave non servirebbe a nulla, perché non permetterebbe di decifrare nessun messaggio.

Quando Alice riceve il messaggio, essa può decrittarlo usando la propria chiave privata (che lei sola conosce e possiede). In questo modo si è risolto di fatto il problema dello scambio delle chiavi e la sicurezza del sistema (almeno in teoria) è perfetta. Infatti non è possibile in alcun modo ricavare la conoscenza della chiave privata a partire da quella pubblica e perciò conoscere la chiave pubblica non è in alcun modo utile a chi volesse provare a craccare l'algoritmo. 

Online RSA Key Generator: un sito online per generare automaticamente una coppia di chiavi pubblica e privata

pidCrypt: cifrare e decifrare con l'algoritmo RSA

 

precedente - successiva

Sito realizzato in base al emplate offerto da

http://www.graphixmania.it

Segui @ElePrograMania