Whitfield Diffie e Martin Hellman sono i due crittografi statunitensi che per primi risolsero il problema dello scambio delle chiavi.

Il problema della distribuzione delle chiavi sembrava a Diffie particolarmente interessante: chi lo avesse risolto, sarebbe passato alla storia come uno dei massimi crittografi di ogni tempo.
Diffie, già agli albori della rete Internet, immaginò due estranei che si incontravano via Internet, e si chiese come avrebbero potuto scambiarsi messaggi crittati. Prese in considerazione il caso di una persona che volesse acquistare tramite Internet un prodotto. Come avrebbe potuto inviare un e-mail con i dati crittati della sua carta di credito, in modo che solo il destinatario potesse decifrarli? Sembrava che le parti non potessero fare a meno di concordare una chiave, ma come riuscirci in condizioni di sicurezza? Il numero di scambi occasionali di comunicazioni e di e-mail tra gli utenti della rete sarebbe stato enorme, e altrettanto difficile sarebbe stata la distribuzione delle chiavi.
Nel 1974 egli fece visita al Laboratorio Watson dell’IBM della Columbia University di New York, dov’era stato invitato a tenere una conferenza. Parlò di varie strategie di attacco relative al problema della distribuzione delle chiavi, ma tutte le sue idee erano in uno stadio iniziale di elaborazione, e l’uditorio le accolse con scetticismo. Alan Konheim, uno dei crittografi esperti dell’IBM accennò al fatto che recentemente un altro studioso aveva visitato il laboratorio e tenuto una conferenza e anch’egli aveva tentato di affrontare il problema della distribuzione delle chiavi. Il relatore era Martin Hellman, un professore dell’università californiana di Stanford. Quella sera Diffie prese la sua automobile e affrontò un viaggio di cinquemila chilometri fino alla costa occidentale per incontrare la sola persona che sembrava condividere la sua ossessione.
L’alleanza di Diffie e Hellman avrebbe generato una delle collaborazioni più dinamiche nella storia della crittografia.
“Se si vuole arrivare da qualche parte compiendo ricerche originali, bisogna essere un po’ matti; solo i folli non si stancano di tentare. Ti viene l’idea numero 1, ci speri, e si rivela un fallimento. Allora provi l’idea numero 2, ci speri, e ti delude… Poi ti viene l’idea numero 99, ci speri, e anche quella ti delude. Solo un pazzo può lasciarsi tentare dalla centesima idea. Eppure, può accadere di doverne scartare novantanove per trovare quella che dà frutto. Se non si è abbastanza matti da continuare a entusiasmarsi, la motivazione vien meno, e non si può proseguire. Dio ripaga i folli.″
Se due persone vogliono usare il telefono per condividere un segreto, il mittente deve crittarlo. Per crittarlo deve ricorrere a una chiave, che è a sua volta un segreto. Sorge quindi il problema di trasmettere la chiave, per poter trasmettere il messaggio. In breve, per potere condividere un segreto (tramite un messaggio crittato), due persone dovrebbero già condividere un segreto (la chiave).
Per ragionare di distribuzione delle chiavi, è utile riferirsi ad Alice, Bob ed Eva, tre personaggi immaginari spesso utilizzati nelle discussioni sulla crittografia commerciale. Di solito Alice vuole mandare un messaggio a Bob, o viceversa, ed Eva vuole conoscerne il contenuto. Per impedire a Eva di scoprire cose che non la riguardano, Alice decide di crittare ogni messaggio con una chiave diversa prima di mandarlo a Bob (cambia la chiave di cifratura a ogni invio).
Ma ogni volta deve affrontare il problema del recapito della chiave. Una possibile soluzione sarebbe che Alice e Bob si incontrassero una volta alla settimana e si scambiassero abbastanza chiavi per i messaggi dei sette giorni successivi. Scambiarsi le chiavi brevi manu è un sistema sicuro ma esposto a contrattempi. Per incepparlo, basta una malattia che costringa a letto Alice o Bob per qualche tempo. Oppure, Alice e Bob potrebbero rivolgersi a un corriere; questo li solleverebbe da molti problemi, ma sarebbe più costoso e meno sicuro. Nell’un caso e nell’altro la distribuzione delle chiavi sembra inevitabile.
Da duemila anni, il problema della distribuzione delle chiavi sembrava insuperabile. Eppure, Diffie e Hellman avevano escogitato una storiella che offriva qualche indizio per una possibile soluzione.
L’immaginaria vicenda, in cui ritroviamo Bob e Alice, è ambientata in un Paese in cui il servizio postale ètotalmente inaffidabile. I suoi dipendenti infatti si divertono a leggere tutta la corrispondenza, aprendo tutte le lettere inviate.
Un giorno Bob, dovendo inviare a Alice un messaggio personale, decide di collocarlo in una scatola di metallo chiusa da un lucchetto. Ovviamente, egli non ha intenzione di consegnare all’impiegato delle poste sia la scatola che la chiave. Consegnando solo la scatola, il messaggio giungerà a Alice in condizioni di sicurezza; ma come farà Alice ad aprire il lucchetto? Per un attimo, Bob pensa di collocare la chiave in un altra scatola con lucchetto e di spedirla a Alice. Ma poiché lei non ha nemmeno la chiave del secondo lucchetto, ciò non rappresenterebbe un passo avanti. Non sembrano esserci alternative: per uscire dall’impasse Bob deve fare una copia della chiave e consegnarla a Alice in anticipo, magari durante la pausa per il caffè. Siamo tornati al vecchio problema della distribuzione. Evitarlo sembra impossibile per ragioni logiche: se Bob chiude la scatola con un lucchetto, in modo che solo Alice possa prendere visione del contenuto, Alice deve possedere una copia della chiave. In termini crittografici: o Alice conosce la chiave usata da Bob per crittare il messaggio, o quest’ultimo gli sarà incomprensibile (a meno che si improvvisi crittoanalista).
Immaginate ora la seguente situazione. Come prima, Bob vuole mandare a Alice un messaggio molto personale. Di nuovo, lo colloca in una scatola metallica, chiude la scatola con un lucchetto, e la spedisce a Alice tenendosi però la chiave. Ricevuta la scatola, Alice non può aprirla (non possiede infatti la chiave per aprire il lucchetto applicato da Bob). Invece Alice applica alla scatola un secondo lucchetto (del quale solo lei possiede la chiave) e la rispedisce a Bob. Quando Bob riceve la scatola, può rimuovere il primo lucchetto (quello che ha messo lui) e di rispedirla a Alice; infatti il lucchetto di Alice è sufficiente ad assicurare l’inviolabilità del contenuto. Quando la scatola è finalmente recapitata a Alice, lei può aprire il secondo lucchetto con la sua chiave, da cui non si è mai separata.
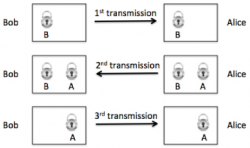
Le implicazioni di questo breve racconto sono profonde. Esso dimostra che un messaggio segreto può essere trasmesso da una persona a un’altra in modo sicuro, senza dover necessariamente recapitare la chiave. Per la prima volta, disponiamo di uno schema in cui la distribuzione delle chiavi non è parte integrante della crittografia. Il racconto può essere reinterpretato in termini di cifratura. Bob usa la propria chiave per crittare il messaggio destinato a Alice. Alice lo ricritta usando anch’egli la propria chiave, e lo rimanda a Bob. Bob rimuove dal messaggio bi-crittato la propria cifratura, e lo invia a Alice in forma mono-crittata. Infine, Alice rimuove la sua cifratura, e legge il messaggio.
Sito realizzato in base al emplate offerto da
http://www.graphixmania.it