In generale la forma di un segnale sonoro Ŕ estremamente complessa e non pu˛ essere ricondotta a nessuna forma d'onda elementare. Inoltre non si tratta neppure in generale di un segnale periodico. Per esempio la figura seguente mette a confronto il segnale sonoro che corrisponde al suono di una singola corda di chitarra e a un colpo di percussioni nell'orchestra:
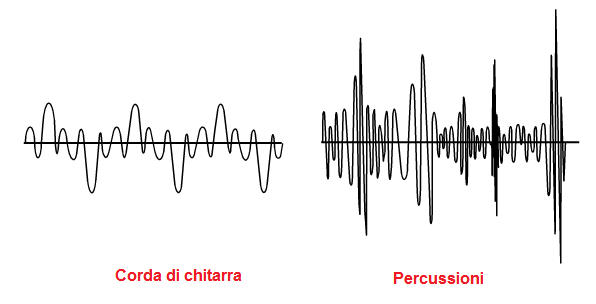
Tuttavia ci sono alcuni tipi di suono molto semplici che possono essere rappresentati con semplici forme d'onda. Si tratta dei cosiddetti toni puri o suoni puri. In natura non esistono molti esempi di toni puri: il diapason usato per accordare gli strumenti musicali, quando viene percosso produce un suono che, con buona approssimazione, si avvicina ad un tono puro. Anche i sintetizzatori elettronici sono in grado di produrre suoni praticamente puri.
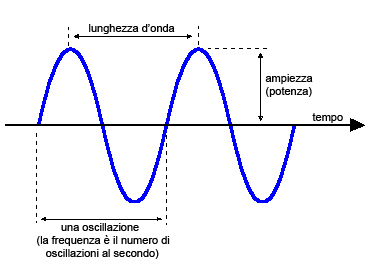
Un tono puro produce un'onda sonora perfettamente sinusoidale e dunque interamente caratterizzabile da tre parametri:
- l'ampiezza, cioè il valore massimo dell'onda (a sua volta legato alla potenza sonora dell'onda stessa);
- la frequenza, cioè il numero di oscillazioni al secondo dell'onda;
- la lunghezza d'onda, cioè la distanza nello spazio fra due creste successive (legato alla velocità di propagazione dell'onda nel mezzo trasmissivo).
Dal punto di vista della percezione umana, i due parametri fondamentali sono l'ampiezza e la frequenza del tono puro.
Ampiezza e volume
L'ampiezza di un tono puro sinusoidale viene percepito dall'orecchio come volume o intensità sonora. Maggiore è l'ampiezza dell'onda, maggiore sarà il volume sonoro percepito.
Si definisce soglia di udibilità la minima intensità sonora che l'orecchio umano è in grado di percepire. L'esperienza mostra che tale soglia varia da individuo a individuo (per esempio si innalza all'aumentare dell'età del soggetto), e, soprattutto che, anche per un singolo individuo, essa dipende dalla frequenza del suono ascoltato.
Il livello di intensità sonora si misura in decibel di pressione sonora (dBSPL o pi¨ brevemente dB). L'intensità sonora IdB è definta come
IdB= 10 log10 (I/I0)
dove I0 è un valore convenzionale, ottenuto mediando la soglia di udibilità di molti individui per un suono puro di frequenza di 1000 Hz. Esso vale
I0 = 10-12 W/m2
Il rapporto I/I0 Ŕ un numero puro e la misura in dB rappresenta quanto l'intensitÓ sonora risulta maggiore rispetto alla soglia di udibilitÓ. La tabella seguente riporta l'intensitÓ sonora associata a diversi eventi:
| dBSPL | Sorgente | Numero di volte rispetto all'udibilitÓ |
|---|---|---|
| 300 | Eruzione del Krakatoa nel 1883 | 1030 |
| 250 | All'interno di un tornado | 1025 |
| 180 | Razzo al decollo | 1018 |
| 140 | Colpo di pistola a 1 m | 1014 |
| 130 | Soglia del dolore | 1013 |
| 125 | Aereo al decollo a 50 m | 1012,5 |
| 120 | Sirena, Auto di Formula 1 in pista | 1012 |
| 110 | Motosega a 1 m | 1011 |
| 100 | Discoteca, concerto rock | 1010 |
| 90 | Urlo, fischietto | 109 |
| 80 | Camion pesante a 1 m | 108 |
| 70 | Aspirapolvere a 1 m; radio ad alto volume | 107 |
| 60 | Ufficio rumoroso, radio, conversazione | 106 |
| 50 | Ambiente domestico; teatro a 10 m | 105 |
| 40 | Quartiere abitato, di notte | 104 |
| 30 | Sussurri a 1 m | 1000 |
| 20 | Respiro umano | 100 |
| 0 | Soglia dell'udibile | 1 |
| -9 | Camera anecoica | 0,13 |
Osserviamo che i dB forniscono una scala logaritmica per la misura dell'intensitÓ sonora: ad ogni aumento di 10 dB corrisponde un aumento di un fattore 10 dell'intensitÓ del suono.
L'adozione di tale scala trova giustificazione nel fatto che l'orecchio umano non presenta una sensibilitÓ lineare rispetto all'intensitÓ sonora, ma, in prima approssimazione, la sensibilitÓ cresce in modo logaritmico rispetto all'intensitÓ (cioŔ secondo la scala in dB).
Frequenza e altezza
La frequenza di un tono puro viene percepito come altezza della nota: note di diversa altezza corrispondono a toni con frequenza diversa. In pratica il termine altezza usato in musica corrisponde alla frequenza misurata della nota.
Ad esempio, la frequenza corrispondente alla nota LA posta al centro della tastiera del pianoforte è pari a 440 Hz. La figura seguente mostra la frequenza corrispondente ad alcune note sul pentagramma musicale:

I valori esatti sono i seguenti:
|
Do 4 |
261,6 Hz |
|
Do # = Re b |
277,2 Hz |
|
Re |
293,7 Hz |
|
Re # |
311,1 Hz |
|
Mi |
329,6 Hz |
|
Fa |
349,2 Hz |
|
Fa # |
370,0 Hz |
|
Sol |
392 Hz |
|
Sol # |
415,3 Hz |
|
La |
440 Hz |
|
La # |
466,2 Hz |
|
Si |
493,9 Hz |
|
Do 5 |
523,3 Hz |
Notiamo che al crescere della frequenza i suoni divengono sempre più acuti. Dunque l'altezza (= frequenza) è una caratteristica del suono che consente di ordinare i suoni in una scala da gravi (o bassi) ad acuti (o alti).
Inoltre fra due note uguali appartenenti a due ottave successive (es. DO 4 d DO 5) la frequenza raddoppia: dunque il concetto musicali di ottava corrisponde a un raddoppio in frequenza.
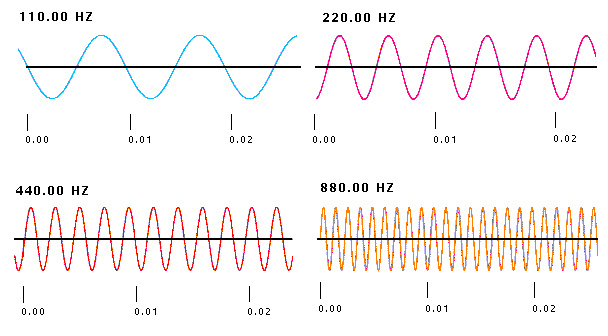
La figura qui sotto mostra toni puri di altezza (cioè di frequenza) diverse ma con la stessa ampiezza:
Sito realizzato in base al template offerto da
http://www.graphixmania.it